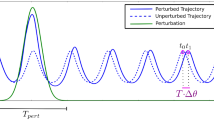
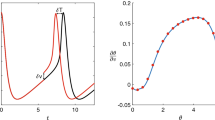
Abstract
Phase resetting curves (PRCs) provide a measure of the sensitivity of oscillators to perturbations. In a noisy environment, these curves are themselves very noisy. Using perturbation theory, we compute the mean and the variance for PRCs for arbitrary limit cycle oscillators when the noise is small. Phase resetting curves and phase dependent variance are fit to experimental data and the variance is computed using an ad-hoc method. The theoretical curves of this phase dependent method match both simulations and experimental data significantly better than an ad-hoc method. A dual cell network simulation is compared to predictions using the analytical phase dependent variance estimation presented in this paper. We also discuss how entrainment of a neuron to a periodic pulse depends on the noise amplitude.










Similar content being viewed by others
References
Abouzeid, A., & Ermentrout, B. (2009). Type-ii phase resetting curve is optimal for stochastic synchrony. Physical Review E, 80, 011911.
Achuthan, S., & Canavier, C. C. (2009). Phase-resetting curves determine synchronization, phase locking, and clustering in networks of neural oscillators. The Journal of Neuroscience, 29(16), 5218–5233.
Ariaratnam, J. T., & Strogatz, S. H. (2001). Phase diagram for the winfree model of coupled nonlinear oscillators. Physical Review Letters, 86, 4278–4281.
Brown, E., Moehlis, J., & Holmes, P. (2004). On the phase reduction and response dynamics of neural oscillator populations. Neural Computation, 16, 673–715.
Dorval, A. D., Christini, D. J., & White, J. A. (2001). Real-time linux dynamic clamp: A fast and flexible way to construct virtual ion channels in living cells. Annals of Biomedical Engineering, 29, 897–907.
Ermentrout, B., & Saunders, D. (2006). Phase resetting and coupling of noisy neural oscillators. Journal of Computational Neuroscience, 20, 179–190.
Forger, D. B., & Paydarfar, D. (2004). Starting, stopping, and resetting biological oscillators: In search of optimum perturbations. Journal of Theoretical Biology, 230, 521–532.
Galan, R. F., Ermentrout, G. B., & Urban, N. N. (2005). Efficient estimation of phase-resetting curves in real neurons and its significance for neural-network modeling. Physical Review Letters, 94, 158101.
Gardiner, C. W. (2004). Handbook of stochastic methods for physics, chemistry and the natural sciences. Springer Series in Synergetics (Vol. 13). Berlin: Springer.
Goel, P., & Ermentrout, B. (2002). Synchrony, stability, and firing patterns in pulse-coupled oscillators. Physica D, 163(3), 191–216.
Golomb, D., & Amitai, Y. (1997). Propagating neuronal discharges in neocortical slices: Computational and experimental study. Journal of Neurophysiology, 78, 1199–1211.
Guevara, M. R., & Glass, L. (1982). Phase locking, period doubling bifurcations and chaos in a mathematical model of a periodically driven oscillator: A theory for the entrainment of biological oscillators and the generation of cardiac dysrhythmias. Journal of Mathematical Biology, 14, 1–23.
Harris, J. J., & Stocker, H. (1998). Handbook of mathematics and computational science. New York: Springer.
Ito, K. (1946). On a stochastic integral equation. Proceedings of the Japan Academy, 22, 32–35.
Kloeden, P. E., & Platen, E. (1992). Numerical solution of stochastic differential equations. Applications of Mathematics (New York) (Vol. 23). Berlin: Springer.
Kuramoto, Y. (1984). Chemical oscillations, waves, and turbulence. Dover Publications.
Ly, C., & Ermentrout, G. B. (2009). Synchronization dynamics of two coupled neural oscillators receiving shared and unshared noisy stimuli. Journal of Computational Neuroscience, 26, 425–443.
Ly, C., & Ermentrout, G. B. (2010). Coupling regularizes individual units in noisy populations. Physical Review E, 81, 11911.
Netoff, T. I., Acker, C. D., Bettencourt, J. C., & White, J. A. (2005a). Beyond two-cell networks: Experimental measurement of neuronal responses to multiple synaptic inputs. Journal of Computational Neuroscience, 18, 287–295.
Netoff, T. I., Banks, M. I., Dorval, A. D., Acker, C. D., Haas, J. S., Kopell, N., et al. (2005b). Synchronization in hybrid neuronal networks of the hippocampal formation. Journal of Neurophysiology, 93, 1197–1208.
Neu, J. C. (1979). Coupled chemical oscillators. SIAM Journal on Applied Mathematics, 37(2), 307–315.
Pervouchine, D. D., Netoff, T. I., Rotstein, H. G., White, J. A., Cunningham, M. O., Whittington, M. A., et al. (2006). Low-dimensional maps encoding dynamics in entorhinal cortex and hippocampus. Neural Computation, 18, 2617–2650.
Plackett, R. L. (1983). Karl pearson and the chi-squared test. International Statistical Review, 51, 59–72.
Preyer, A., & Butera, R. (2005). Neuronal oscillators in aplysia californica that demonstrate weak coupling in vitro. Physical Review Letters, 95(13), 138103.
Reyes, A. D., & Fetz, E. E. (1993). Effects of transient depolarizing potentials on the firing rate of cat neocortical neurons. Journal of Neurophysiology, 69, 1673–1683.
Stoop, R., Schindler, K., & Bunimovich, L. A. (2000). Neocortical networks of pyramidal neurons: From local locking and chaos to macroscopic chaos and synchronization. Nonlinearity, 13, 1515–1529.
Torben-Nielsen, B., Uusisaari, M., & Stiefel, K. (2010). A comparison of methods to determine neuronal phase-response curves. Frontiers in Neuroinformatics, 4(6).
Welch, B. L. (1947). The generalization of student’s problem when several different population variances are involved. Biometrika, 34, 28–35.
Winfree, A. T. (1967). Biological rhythms and the behavior of populations of coupled oscillators. Journal of Theoretical Biology, 16, 15–42.
Acknowledgements
We would like to acknowledge NSF, NSF CAREER Award, and University of Minnesota Grant-in-Aid.
Author information
Authors and Affiliations
Corresponding author
Additional information
Action Editor: Charles Wilson
Rights and permissions
About this article
Cite this article
Ermentrout, G.B., Beverlin, B., Troyer, T. et al. The variance of phase-resetting curves. J Comput Neurosci 31, 185–197 (2011). https://doi.org/10.1007/s10827-010-0305-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10827-010-0305-9